神经单元 Neural Unit
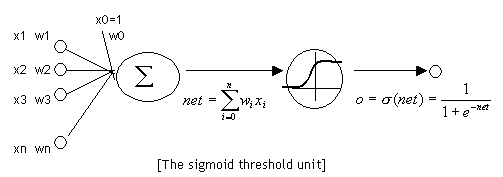
- 一个神经单元可以接受多个输入:x1,x2…xn,和一个偏执项b
- 神经单元的输出计算公式为:$f(x)=w^Tx+b$
- 最后是一个激活函数,这里使用Sigmod函数
全连接神经网络 Full-Connection Neural Network
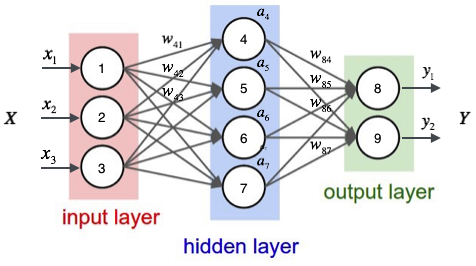
计算隐藏层第一层
计算输出层
反向传播 Back Propagetion
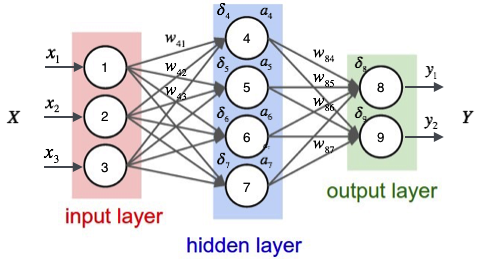
已有数据 Given Data
矩阵表示 matrix indicate
损失函数 Cost Function
计算 $\mathbf{\Large {\frac{\Delta{E_d}}{\Delta{w}}}}$
$w_{ji}$只可能通过j层影像其他部分,设是节点$net_j$的加权输入
$E_d$是$net_j$的函数,$net_j$而是$w_{ji}$的函数。根据链式求导法则:
计算 $\mathbf{ \Large {\frac{\Delta{E_d}}{\Delta{net_j}}} }$
现在只需要做$\frac{\Delta{E_d}}{\Delta{net_j}}$的推导:
输出层时
- 输出层,$net_j$ 只能通过节点j的输出值$y_j$来影响其他部分
- 也就是$E_d$是$y_j$的函数,而$y_j$是$net_j$的函数
- 其中$y_j=sigmoid(net_j)$
- 可以使用链式求导法则:
声明临时变量
利用EX5进行递归操作
隐藏层时
- 首先定义节点$j$的所有直接下游节点集合$DownStream(j)$
- 所有$net_j$只能通过影响$DownStream(j)$再影响$E_d$
- 若$net_k$为$j$的下游节点输入
- 则$E_d$是$net_k$的函数,$net_k$是$net_j$的函数
- $a_i$是节点的输出值
- 因为$net_k$有多个,使用全导数公式进行推导:
声明临时变量
最后得到
梯度下降 Grendient Dscent
程序实现
使用numpy实现双层神经网络
# -*- coding: utf-8 -*-
import numpy as np
# N is batch size; D_in is input dimension;
# H is hidden dimension; D_out is output dimension.
N, D_in, H, D_out = 64, 1000, 100, 10
# Create random input and output data
x = np.random.randn(N, D_in)
y = np.random.randn(N, D_out)
# Randomly initialize weights
w1 = np.random.randn(D_in, H)
w2 = np.random.randn(H, D_out)
learning_rate = 1e-6
for t in range(500):
# Forward pass: compute predicted y
h = x.dot(w1)
h_relu = np.maximum(h, 0)
y_pred = h_relu.dot(w2)
# Compute and print loss
loss = np.square(y_pred - y).sum()
print(t, loss)
# Backprop to compute gradients of w1 and w2 with respect to loss
grad_y_pred = 2.0 * (y_pred - y)
grad_w2 = h_relu.T.dot(grad_y_pred)
grad_h_relu = grad_y_pred.dot(w2.T)
grad_h = grad_h_relu.copy()
grad_h[h < 0] = 0
grad_w1 = x.T.dot(grad_h)
# Update weights
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2
代码参考 https://github.com/hanbt/learn_dl/blob/master/bp.py