卷积神经网络

Refrence Math Formula

Relu Activation Function

卷积神经网络选择Relu函数作为卷基层的激活函数

$$f(x)= max(0,x) [\mathbf{MF01}]$$

Two-dimantional Covolution Formula

$$\begin{aligned} C_{s,t}&=\sum_0^{m_a-1}\sum_0^{n_a-1} A_{m,n}B_{s-m,t-n} [\mathbf{MF02}] \end{aligned}$$

• 矩阵A,B的行列数分别为$m_a,n_a,m_a,m_b$
• s,t满足$0\le{s}\lt{m_a+m_b-1}, 0\le{t}\lt{n_a+n_b-1}$
  

  此公式可以简写为

$$C = A * B [\mathbf{MF03}]$$

Introduction Convelutional Neural Network

Three Lays

• N 为卷积层的数量
• M 为池化层的数量
• K 为全连接层数量

流程：INPUT -> CONVN -> POOLM -> FC*K

Convelutional Layer

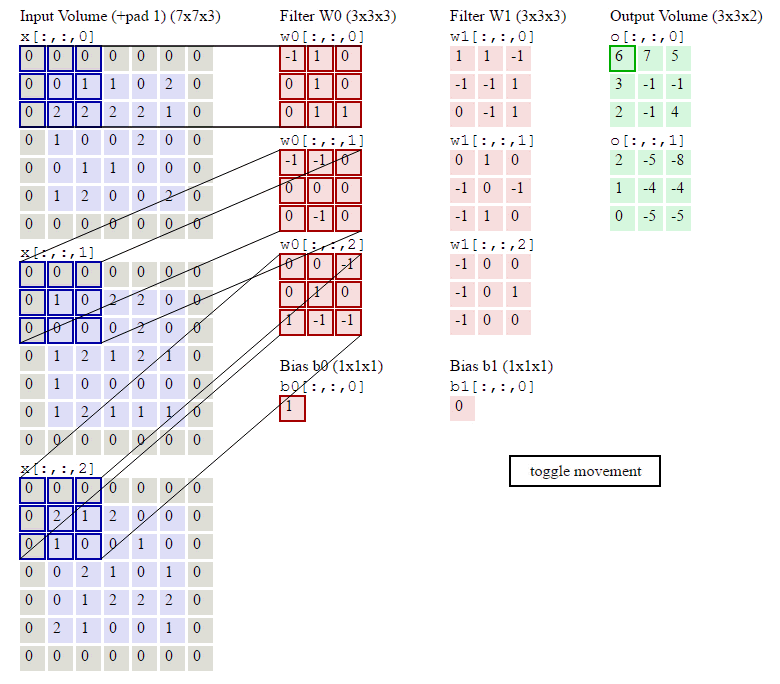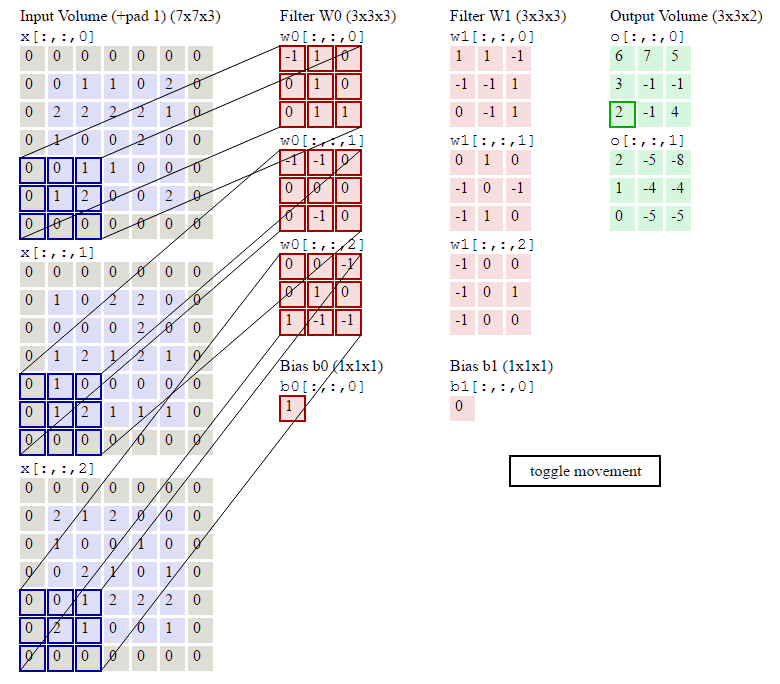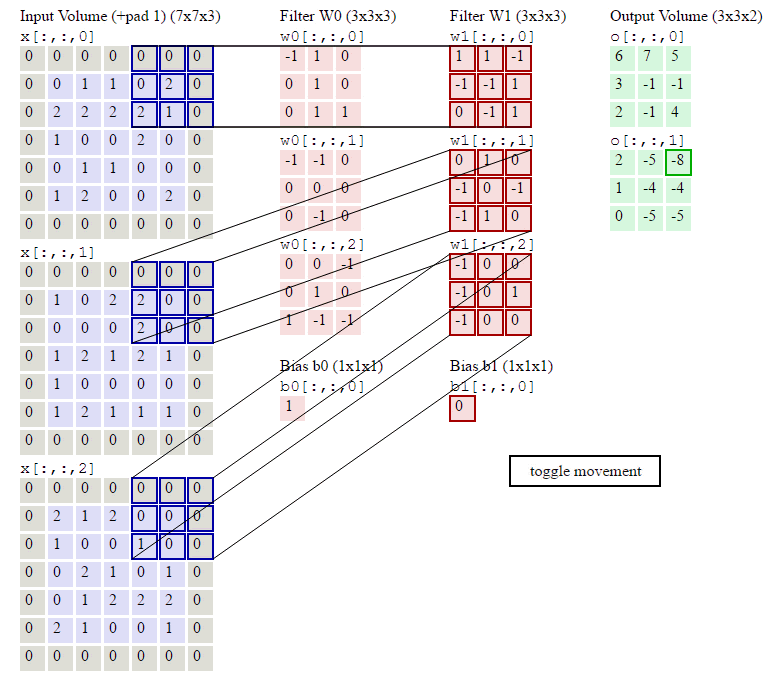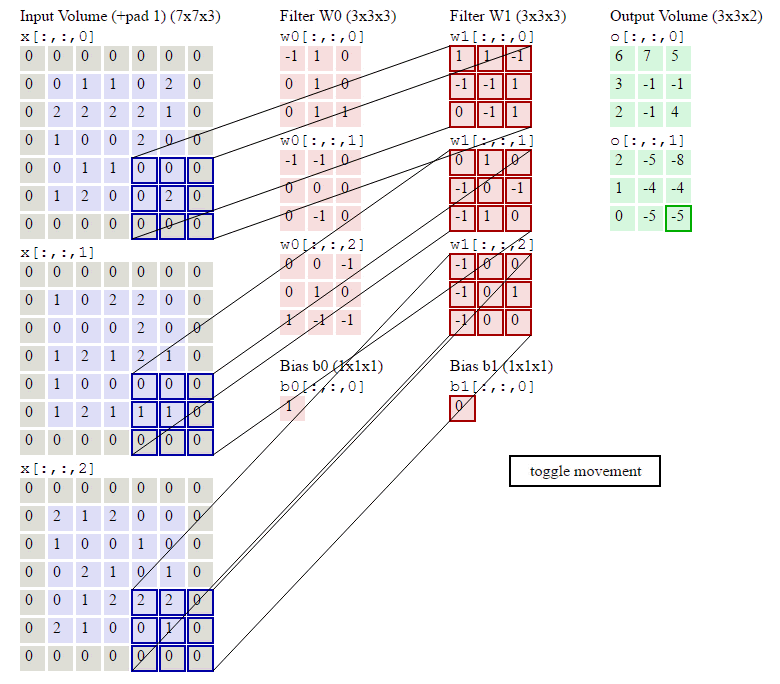
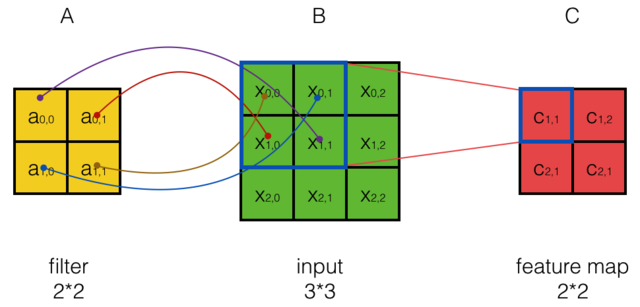
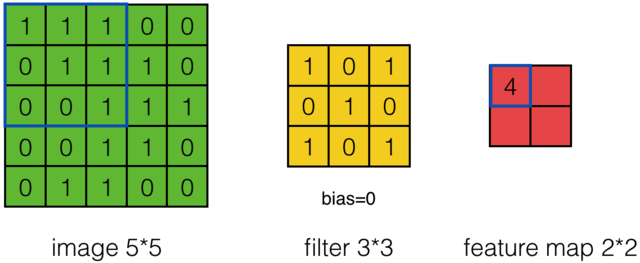
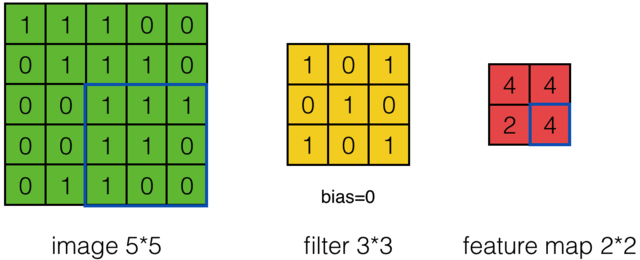
Input Matix，Filter Matrix，Feature Map Matrix

输入矩阵，特征筛选矩阵，输出矩阵(特征映射矩阵)如下：

• $X_{ij}$表示Input矩阵的i行，第j列
• $W_{mn}$表示Filter矩阵的m行，第n列
• $W_{b}$表示Filter矩阵的偏执项
• $a_{ij}$表示Feature Map矩阵的m行，第n列
• $f$为激活函数Relu
• 步幅为1

  Calculate Feature Map Matrix’s Width & Height

  输出矩阵的高度和宽度计算公式为：

$$\begin{aligned} W_2 &= (W_1 - F + 2P)/S + 1\\ H_2 &= (H_1 - F + 2P)/S + 1 \end{aligned}$$

• $W_1$为输入矩阵的宽度，$H_1$为输入矩阵的高度
• $W_1$为Feature Map 矩阵的宽度，$H_1$为Feature Map 矩阵的高度
• $F$为Filter矩阵的宽度
• $P$为Zero Padding的圈数，补0的圈数
• $S$为步幅
• 示例见 [EX01]

Calculate Feature Map Element

$$a_{i,j}=f(\sum_{d=0}^{D-1}\sum_{m=0}^{F-1}\sum_{n=0}^{F-1}w_{d,m,n}x_{d,i+m,j+n}+w_b) [\mathbf{MF01}] [\mathbf{RP01}]$$

Calculate Feature Map Matrix

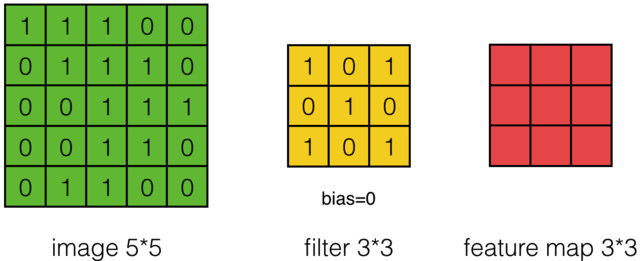
卷积和互相关操作是可以转化的,把矩阵A翻转180度，然后再交换A和B的位置（即把B放在左边而把A放在右边。卷积满足交换率，这个操作不会导致结果变化），那么卷积就变成了互相关,得到输出矩阵的公式：

$$A=f(\sum_{d=0}^{D-1}X_d*W_d+w_b) [\mathbf{USING\ MF03,MF04}]$$

如下图计算示例：

Pooling Layer Calculate

Pooling的层的主要作用是下采样，主要有两种方式Max Pooling 和Mean Pooling

• Max Pooling是取n*n中的U最大值
  
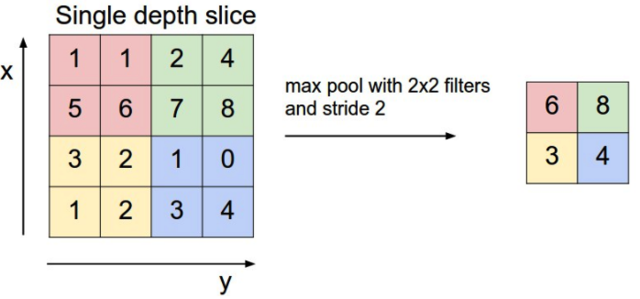
• Mean Pooling是取n*n中的平均值

Full Connection Layer

参考Neural Network

Train Convolutional Neural Network

卷积神经网络训练依旧采用反向传播训练方法 Train Step

• 向前计算每个神经元的输出值$a_j$
• 反向计算每个神经元的误差项$\delta_j$

• $\delta_j$也成为敏感度，是损失函数$E_d$对神经元加权输入$net_j$的偏导数$\delta_j=\frac{\partial{E_d}}{\partial{net_j}}$

• 计算每个神经元$w_ji$的梯度

• $w_ji$标示神经元i连接到神经元j的权重，公式为$\frac{\partial{E_d}}{\partial{w_{ji}}}=a_i\delta_j$,$a_i$标示神经元i的输出

• 梯度下降更新每个权重w

  Train Convlution Layer

  误差传递

  

$$\begin{aligned} net^l&=conv(W^l, a^{l-1})+w_b\\ a^{l-1}_{i,j}&=f^{l-1}(net^{l-1}_{i,j}) \end{aligned}$$

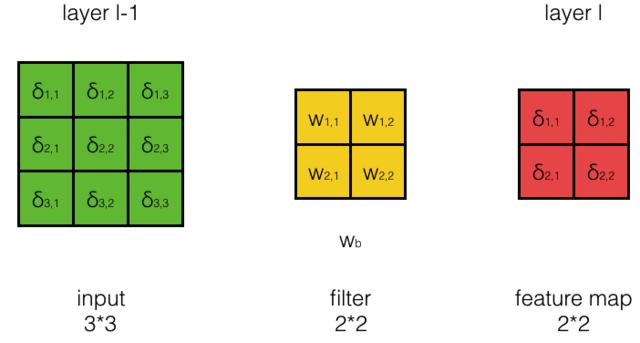
• $\delta^{l-1}_{i,j}$表示第l-1层的第i行，第j列的误差项
• $w_{m,n}$表示Filter 第m行，第n列的权重
• $w_b$表示Filter的偏执项
• $a^{l-1}_{i,j}$表示第l-1层的输出
• $net^{l-1}_{i,j}$表示第l-1层的加权输入
• $net^l$,$W^l$,$a^{l-1}$都是矩阵,conv为卷积操作

Calculate $\mathbf{ \Large { \delta^{l-1}} }$

calculate single element

$$\begin{aligned} \delta^{l-1}_{i,j}=\sum_m\sum_n{w^l_{m,n}\delta^l_{i+m,j+n}}f'(net^{l-1}_{i,j}) \end{aligned}$$

calculate matrix

$$\delta^{l-1}=\sum_{d=0}^D\delta_d^l*W_d^l\circ f'(net^{l-1}) \mathbf{[RP02]}$$

• 第d个Filter Metrax产生第i个Feature Map
• l-1 层的每个加权输入$net^{l-1}_{d, i,j}$,影响了l层的所有Feature Map输出，所以计算误差项，要用全导数公式
• 最后将D个sensitivity map 按元素相加

Calculate $\mathbf{ \Large { \frac{\partial{E_d}}{\partial{w_{i,j}}}} }$

$$\frac{\partial{E_d}}{\partial{w_{i,j}}}=\sum_m\sum_n\delta_{m,n}a^{l-1}_{i+m,j+n}$$ $$\begin{aligned} \frac{\partial{E_d}}{\partial{w_b}}&=\sum_i\sum_j\delta^l_{i,j} \mathbf{[RF03]} \end{aligned}$$

Train Pooling Layer

Max Pooling & Mean Pooling 没有需要学习的参数，只需要计算此层误差的传递，而无剃度的下降

Max Pooling

误差只传递到上一层中对应的最大项中 见[EX04]

Mean Pooling

误差项是平均分配到上一个层的所有神经元 可以使用克罗内克积(Kronecker product)计算：

$$\delta^{l-1} = \delta^l\otimes(\frac{1}{n^2})_{n\times n} \mathbf{[RP05]}$$

• n 是Pooling Layer的Filter Matrix 的大小
• $\delta^{l-1} $，$\delta^{l}$是误差的矩阵

Reasoning Process

01 Reasonig feature map element $\mathbf{a_{i,j}}$

卷积计算为

$$a_{i,j}=f(\sum_{m=0}^{2}\sum_{n=0}^{2}w_{m,n}x_{i+m,j+n}+w_b)$$

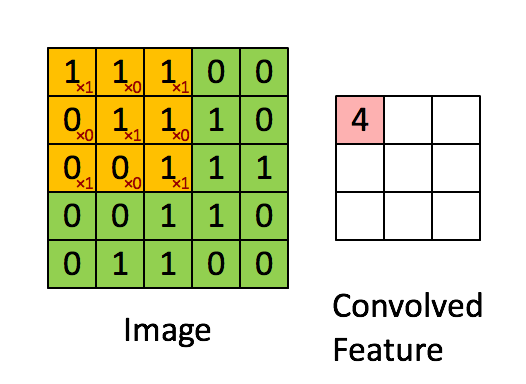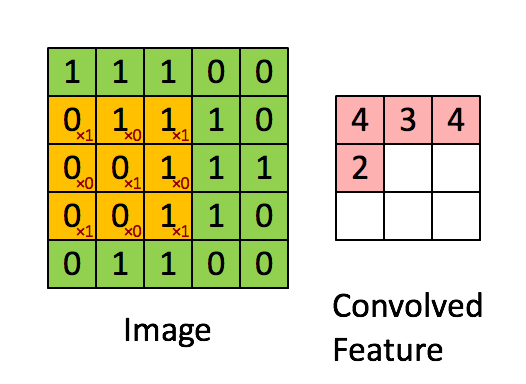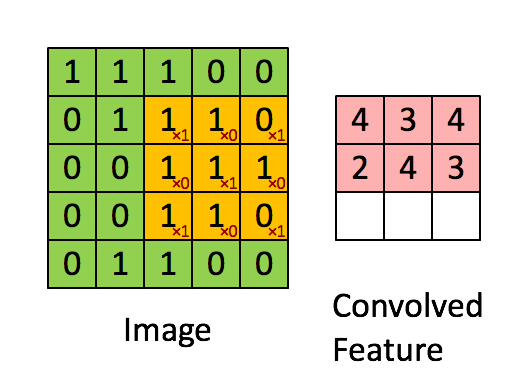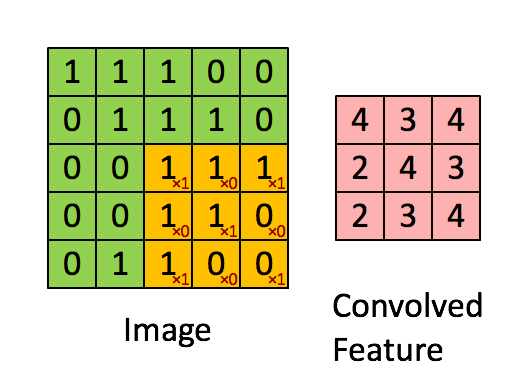
如算输出矩阵的a00：

$$\begin{aligned} a_{0,0}&=f(\sum_{m=0}^{2}\sum_{n=0}^{2}w_{m,n}x_{m+0,n+0}+w_b)\\ &=relu(w_{0,0}x_{0,0}+w_{0,1}x_{0,1}+w_{0,2}x_{0,2}+w_{1,0}x_{1,0}+w_{1,1}x_{1,1}+w_{1,2}x_{1,2}+w_{2,0}x_{2,0}+w_{2,1}x_{2,1}+w_{2,2}x_{2,2}+w_b)\\ &=relu(1+0+1+0+1+0+0+0+1+0)\\ &=relu(4)\\ &=4 \end{aligned}$$

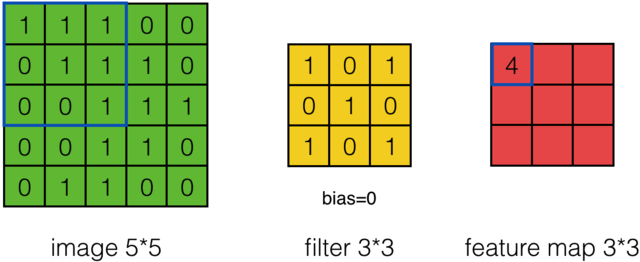
步幅为1是的计算结果如下：

当步幅为2时:

步幅为2时的计算结果如下:

最后得出的卷积通用公式为:

$$a_{i,j}=f(\sum_{d=0}^{D-1}\sum_{m=0}^{F-1}\sum_{n=0}^{F-1}w_{d,m,n}x_{d,i+m,j+n}+w_b)$$

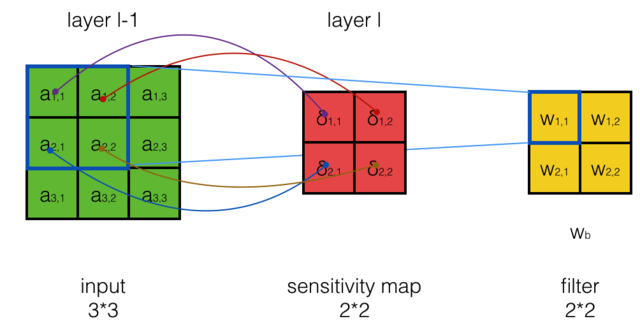
02 Resoning $\mathbf{\delta^{l-1}}$

假设l的每个$\delta^l$都已计算好，计算l-1层的$\delta^{l-1}$

$$\begin{aligned} \delta^{l-1}_{i,j}&=\frac{\partial{E_d}}{\partial{net^{l-1}_{i,j}}}\\ > &=\frac{\partial{E_d}}{\partial{a^{l-1}_{i,j}}}\frac{\partial{a^{l-1}_{i,j}}}{\partial{net^{l-1}_{i,j}}} \end{aligned}$$

先计算第一项$\frac{\partial{E_d}}{\partial{a^{l-1}_{i,j}}}$

$$\frac{\partial{E_d}}{\partial{a^l_{i,j}}}=\sum_m\sum_n{w^l_{m,n}\delta^l_{i+m,j+n}}$$

卷积形式：

$$\frac{\partial{E_d}}{\partial{a_l}}=\delta^l*W^l$$

再计算第二项$\frac{\partial{a^{l-1}{i,j}}}{\partial{net^{l-1}{i,j}}}$

因为：

$$a^{l-1}_{i,j}=f(net^{l-1}_{i,j})$$

所以第二项为f的导数

$$\frac{\partial{a^{l-1}_{i,j}}}{\partial{net^{l-1}_{i,j}}}=f'(net^{l-1}_{i,j})$$

根据第一式和第二式计算

$$\begin{aligned} \delta^{l-1}_{i,j}&=\frac{\partial{E_d}}{\partial{net^{l-1}_{i,j}}}\\ &=\frac{\partial{E_d}}{\partial{a^{l-1}_{i,j}}}\frac{\partial{a^{l-1}_{i,j}}}{\partial{net^{l-1}_{i,j}}}\\ > &=\sum_m\sum_n{w^l_{m,n}\delta^l_{i+m,j+n}}f'(net^{l-1}_{i,j}) \end{aligned}$$

卷积形式：

$$\delta^{l-1}=\delta^l*W^l\circ f'(net^{l-1})$$

• $\circ$表是element-wise product，即矩阵的每个元素相乘
• 式中的$\delta^l$，$\delta^{l-1}$，$net^{l-1}$都是矩阵
  当Filter Matrix的数量为D时，输出的深度也为D

$$\delta^{l-1}=\sum_{d=0}^D\delta_d^l*W_d^l\circ f'(net^{l-1})$$

• 第d个Filter Metrax产生第i个Feature Map
• l-1 层的每个加权输入$net^{l-1}_{d, i,j}$,影响了l层的所有Feature Map输出，所以计算误差项，要用全导数公式
• 最后将D个sensitivity map 按元素相加

03 Resoning $\mathbf{\frac{\partial{E_d}}{\partial{w_b}}}$

推理过程

Example1 :计算$\frac{\partial{E_d}}{\partial{w_{1,1}}}$

$$\begin{aligned} net^j_{1,1}&=w_{1,1}a^{l-1}_{1,1}+w_{1,2}a^{l-1}_{1,2}+w_{2,1}a^{l-1}_{2,1}+w_{2,2}a^{l-1}_{2,2}+w_b \\ net^j_{1,2}&=w_{1,1}a^{l-1}_{1,2}+w_{1,2}a^{l-1}_{1,3}+w_{2,1}a^{l-1}_{2,2}+w_{2,2}a^{l-1}_{2,3}+w_b \\ net^j_{2,1}&=w_{1,1}a^{l-1}_{2,1}+w_{1,2}a^{l-1}_{2,2}+w_{2,1}a^{l-1}_{3,1}+w_{2,2}a^{l-1}_{3,2}+w_b \\ net^j_{2,2}&=w_{1,1}a^{l-1}_{2,2}+w_{1,2}a^{l-1}_{2,3}+w_{2,1}a^{l-1}_{3,2}+w_{2,2}a^{l-1}_{3,3}+w_b \end{aligned}$$

• 由于权值共享,$w_{1,1}$对所有的 $net^l_{i,j}$都有影响
• $E_d$是$net_{1,1}^l$,$net_{1,2}^l$,$net_{2,1}$…的函数
• $net_{1,1}^l$,$net_{1,2}^l$,$net_{2,1}$…是$w_{1,1}$的函数
• 根据全导数公式，计算$\frac{\partial{E_d}}{\partial{w_{1,1}}}$就要把每个全导数加起来

$$\begin{aligned} \frac{\partial{E_d}}{\partial{w_{1,1}}}&=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{w_{1,1}}}+\frac{\partial{E_d}}{\partial{net^{l}_{1,2}}}\frac{\partial{net^{l}_{1,2}}}{\partial{w_{1,1}}}+\frac{\partial{E_d}}{\partial{net^{l}_{2,1}}}\frac{\partial{net^{l}_{2,1}}}{\partial{w_{1,1}}}+\frac{\partial{E_d}}{\partial{net^{l}_{2,2}}}\frac{\partial{net^{l}_{2,2}}}{\partial{w_{1,1}}}\\ &=\delta^l_{1,1}a^{l-1}_{1,1}+\delta^l_{1,2}a^{l-1}_{1,2}+\delta^l_{2,1}a^{l-1}_{2,1}+\delta^l_{2,2}a^{l-1}_{2,2} \end{aligned}$$

Example2 :计算$\frac{\partial{E_d}}{\partial{w_{1,2}}}$

通过$w_{1,2}$和$net_{i,j}^l$的关系，得到：

$$\frac{\partial{E_d}}{\partial{w_{1,2}}}=\delta^l_{1,1}a^{l-1}_{1,2}+\delta^l_{1,2}a^{l-1}_{1,3}+\delta^l_{2,1}a^{l-1}_{2,2}+\delta^l_{2,2}a^{l-1}_{2,3}$$

所以得到通用公式

$$\frac{\partial{E_d}}{\partial{w_{i,j}}}=\sum_m\sum_n\delta_{m,n}a^{l-1}_{i+m,j+n}$$

计算Filter Map Matrix

$$\begin{aligned} \frac{\partial{E_d}}{\partial{w_b}}&=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{w_b}}+\frac{\partial{E_d}}{\partial{net^{l}_{1,2}}}\frac{\partial{net^{l}_{1,2}}}{\partial{w_b}}+\frac{\partial{E_d}}{\partial{net^{l}_{2,1}}}\frac{\partial{net^{l}_{2,1}}}{\partial{w_b}}+\frac{\partial{E_d}}{\ partial{net^{l}_{2,2}}}\frac{\partial{net^{l}_{2,2}}}{\partial{w_b}}\\ &=\delta^l_{1,1}+\delta^l_{1,2}+\delta^l_{2,1}+\delta^l_{2,2}\\ &=\sum_i\sum_j\delta^l_{i,j} \end{aligned}$$

04 calculate max pool loss

IMAGE
Max Pooling的计算方式

$$net^l_{1,1}=max(net^{l-1}_{1,1},net^{l-1}_{1,2},net^{l-1}_{2,1},net^{l-1}_{2,2})$$

每个的偏导数为：

$$\begin{aligned} \frac{\partial{net^l_{1,1}}}{\partial{net^{l-1}_{1,1}}}=1\\ \frac{\partial{net^l_{1,1}}}{\partial{net^{l-1}_{1,2}}}=0\\ \frac{\partial{net^l_{1,1}}}{\partial{net^{l-1}_{2,1}}}=0\\ \frac{\partial{net^l_{1,1}}}{\partial{net^{l-1}_{2,2}}}=0 \end{aligned}$$

所以

$$\begin{aligned} \delta^{l-1}_{1,1}&=\frac{\partial{E_d}}{\partial{net^{l-1}_{1,1}}}\\ &=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{net^{l-1}_{1,1}}}\\ &=\delta^{l}_{1,1}\\ \end{aligned}$$

非最大值的其他项

$$\begin{aligned} \delta^{l-1}_{1,2}&=\frac{\partial{E_d}}{\partial{net^{l-1}_{1,2}}}\\ &=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{net^{l-1}_{1,2}}}\\ &=0\\ \delta^{l-1}_{2,1}&=\frac{\partial{E_d}}{\partial{net^{l-1}_{2,1}}}\\ &=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{net^{l-1}_{2,1}}}\\ &=0\\ \delta^{l-1}_{1,1}&=\frac{\partial{E_d}}{\partial{net^{l-1}_{2,2}}}\\ &=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{net^{l-1}_{2,2}}}\\ &=0\\ \end{aligned}$$

05 calcute mean pool loss

推理过程

IMAGE
Mean Pooling 的计算方式为

$$net^j_{1,1}=\frac{1}{4}(net^{l-1}_{1,1}+net^{l-1}_{1,2}+net^{l-1}_{2,1}+net^{l-1}_{2,2})$$

每个的偏导数为：

$$\begin{aligned} &\frac{\partial{net^l_{1,1}}}{\partial{net^{l-1}_{1,1}}}=\frac{1}{4} \\ &\frac{\partial{net^l_{1,1}}}{\partial{net^{l-1}_{1,2}}}=\frac{1}{4} \\ &\frac{\partial{net^l_{1,1}}}{\partial{net^{l-1}_{2,1}}}=\frac{1}{4} \\ &\frac{\partial{net^l_{1,1}}}{\partial{net^{l-1}_{2,2}}}=\frac{1}{4} \\ \end{aligned}$$

所以可以计算出：

$$\begin{aligned} \delta^{l-1}_{1,1}&=\frac{\partial{E_d}}{\partial{net^{l-1}_{1,1}}}\\ &=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{net^{l-1}_{1,1}}}\\ &=\frac{1}{4}\delta^{l}_{1,1}\\ \end{aligned}$$

同样可以计算出其他项：

$$\begin{aligned} \delta^{l-1}_{1,2}&=\frac{\partial{E_d}}{\partial{net^{l-1}_{1,2}}}\\ &=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{net^{l-1}_{1,2}}}\\ &=\frac{1}{4}\delta^{l}_{1,1}\\ \delta^{l-1}_{2,1}&=\frac{\partial{E_d}}{\partial{net^{l-1}_{2,1}}}\\ &=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{net^{l-1}_{2,1}}}\\ &=\frac{1}{4}\delta^{l}_{1,1}\\ \delta^{l-1}_{2,2}&=\frac{\partial{E_d}}{\partial{net^{l-1}_{2,2}}}\\ &=\frac{\partial{E_d}}{\partial{net^{l}_{1,1}}}\frac{\partial{net^{l}_{1,1}}}{\partial{net^{l-1}_{2,2}}}\\ &=\frac{1}{4}\delta^{l}_{1,1}\\ \end{aligned}$$

误差项是平均分配到上一个层的所有神经元

Calculate Example

01 Calculate feature matrix width and height

如输入宽度为5，特征矩阵宽度为3，Zero Paddding的圈数为0，步幅为2，最后计算的输出矩阵宽度为：

$$\begin{aligned} W_2 &= (W_1 - F + 2P)/S + 1\\ &= (5 - 3 + 0)/2 + 1\\ &=2 \end{aligned}$$

---

• Previous
  神经网络
• Next
  循环神经网络