循环神经网络

Introduction Recurrent Neural Network

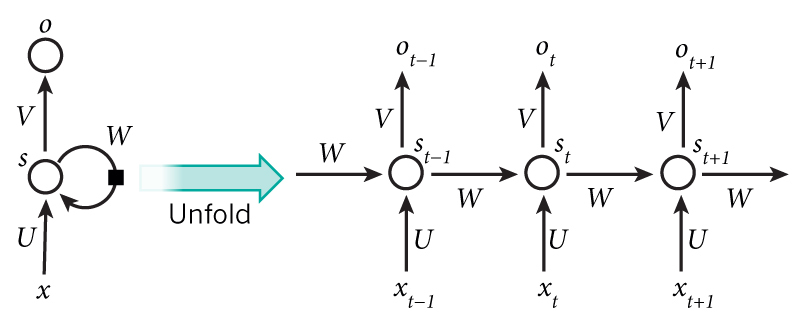
Basic Recutrent Neral Network

循环神经网络也分为两层，Recurrent Layer & Full-Connection Layer

网络在t时刻接收到输入$x_t$之后，隐藏层的值是$s_t$，输出值是$o_t$
关键一点是，网络在t时刻接收到输入的值不仅仅取决于$x_t$，还取决于$s_{t-1}$ 计算方法为

$\begin{aligned} \mathrm{o}_t&=g(V\mathrm{s}_t) \\ \mathrm{s}_t&=f(U\mathrm{x}_t+W\mathrm{s}_{t-1}) \\ \end{aligned}$

输出值的循环计算为：

$\begin{aligned} \mathrm{o}_t&=g(V\mathrm{s}_t)\\ &=Vf(U\mathrm{x}_t+W\mathrm{s}_{t-1})\\ &=Vf(U\mathrm{x}_t+Wf(U\mathrm{x}_{t-1}+W\mathrm{s}_{t-2}))\\ &=Vf(U\mathrm{x}_t+Wf(U\mathrm{x}_{t-1}+Wf(U\mathrm{x}_{t-2}+W\mathrm{s}_{t-3})))\\ &=Vf(U\mathrm{x}_t+Wf(U\mathrm{x}_{t-1}+Wf(U\mathrm{x}_{t-2}+Wf(U\mathrm{x}_{t-3}+...)))) \end{aligned}$

Two-Way Recurrent Neural Network

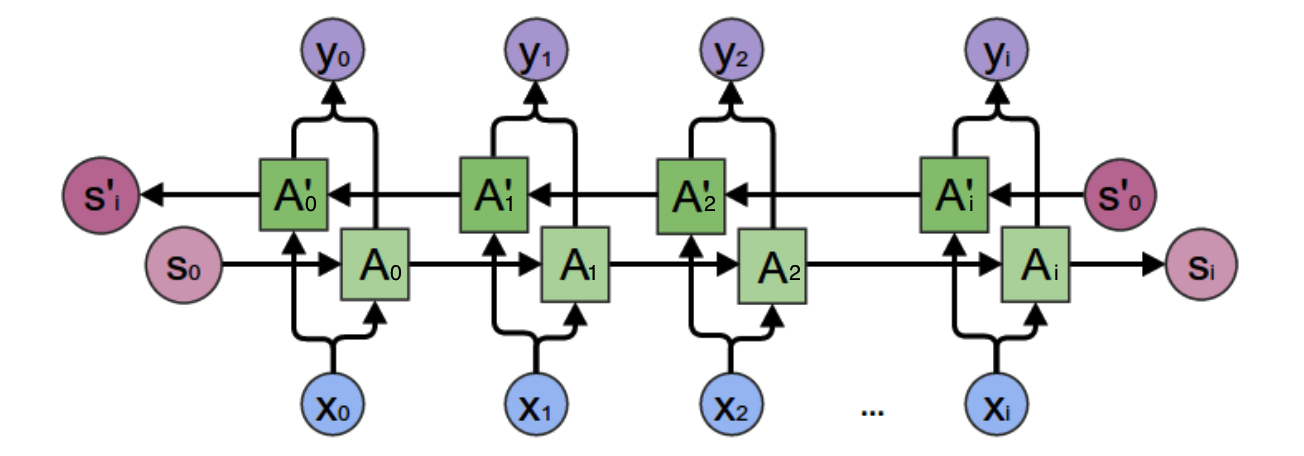
双向循环神经网络，隐藏层要计算两个值，一个是$s_t$正方向的值，一个是${s}_t’$反方向的值计算如下：

$\begin{aligned} \mathrm{o}_t&=g(V\mathrm{s}_t+V'\mathrm{s}_t')\\ \mathrm{s}_t&=f(U\mathrm{x}_t+W\mathrm{s}_{t-1})\\ \mathrm{s}_t'&=f(U'\mathrm{x}_t+W'\mathrm{s}_{t+1}')\\ \end{aligned}$

Deep Recurrent Neural Network

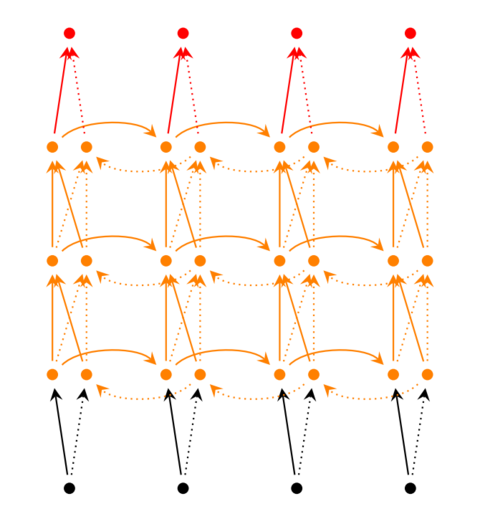
有多个隐藏层的深度循环网络

$\begin{aligned} \mathrm{o}_t&=g(V^{(i)}\mathrm{s}_t^{(i)}+V'^{(i)}\mathrm{s}_t'^{(i)})\\ \mathrm{s}_t^{(i)}&=f(U^{(i)}\mathrm{s}_t^{(i-1)}+W^{(i)}\mathrm{s}_{t-1})\\ \mathrm{s}_t'^{(i)}&=f(U'^{(i)}\mathrm{s}_t'^{(i-1)}+W'^{(i)}\mathrm{s}_{t+1}')\\ ...\\ \mathrm{s}_t^{(1)}&=f(U^{(1)}\mathrm{x}_t+W^{(1)}\mathrm{s}_{t-1})\\ \mathrm{s}_t'^{(1)}&=f(U'^{(1)}\mathrm{x}_t+W'^{(1)}\mathrm{s}_{t+1}')\\ \end{aligned}$

Train Recurrent Neural Network

BPTT(Back Propagation Through Time)算法

前向计算每个神经元的输出值
反向计算每个神经元的误差项值$\delta_j$(误差函数E对神经元j的加权输入$net_j$的偏导数)
计算每个权重的梯度
随机梯度下降更新权重

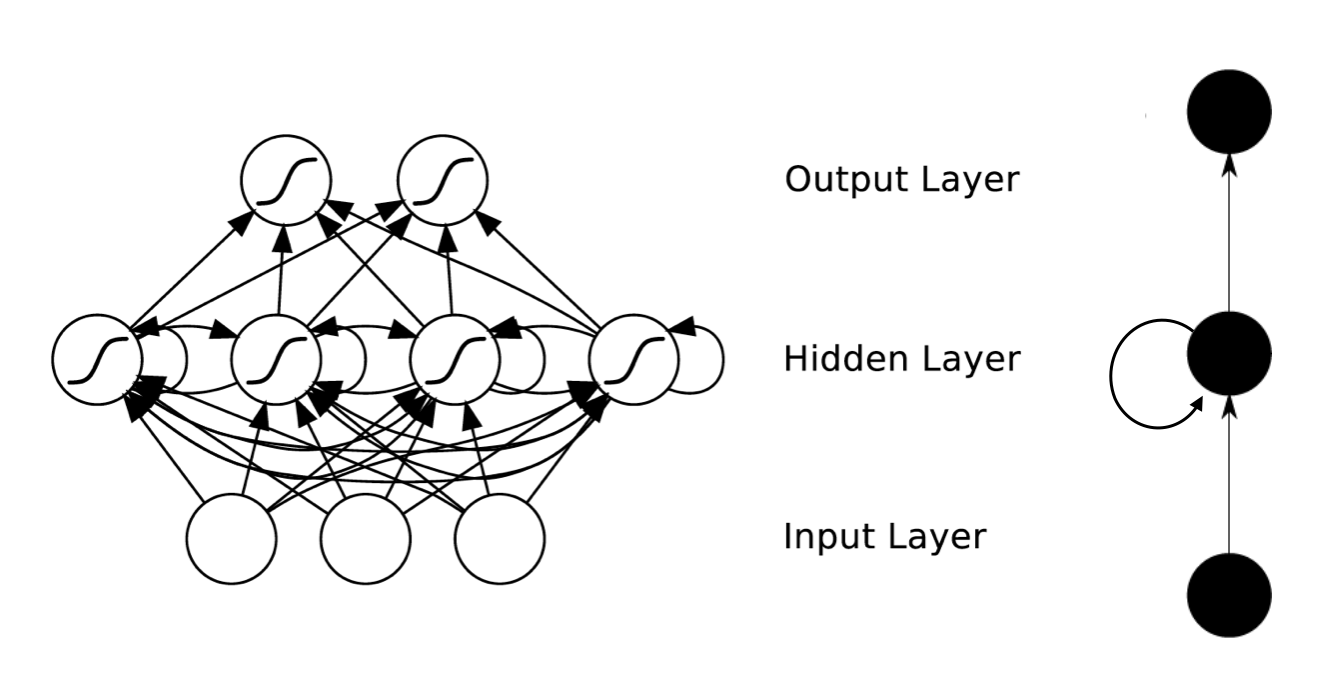
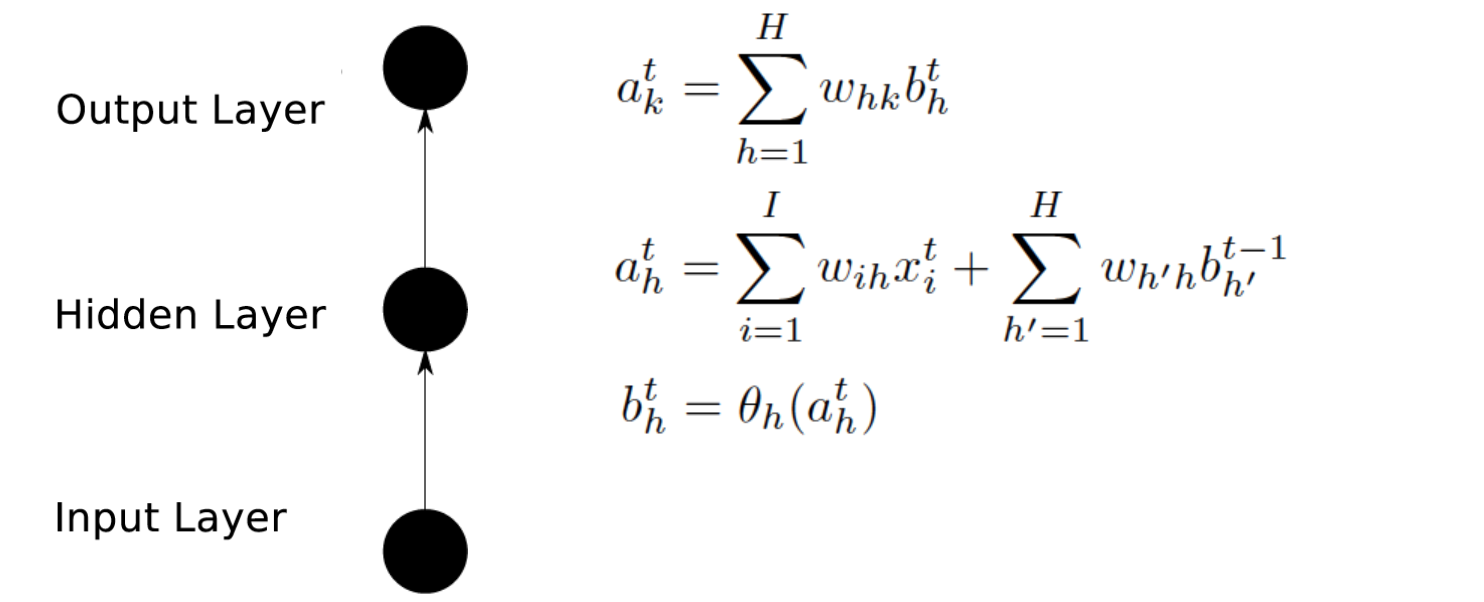
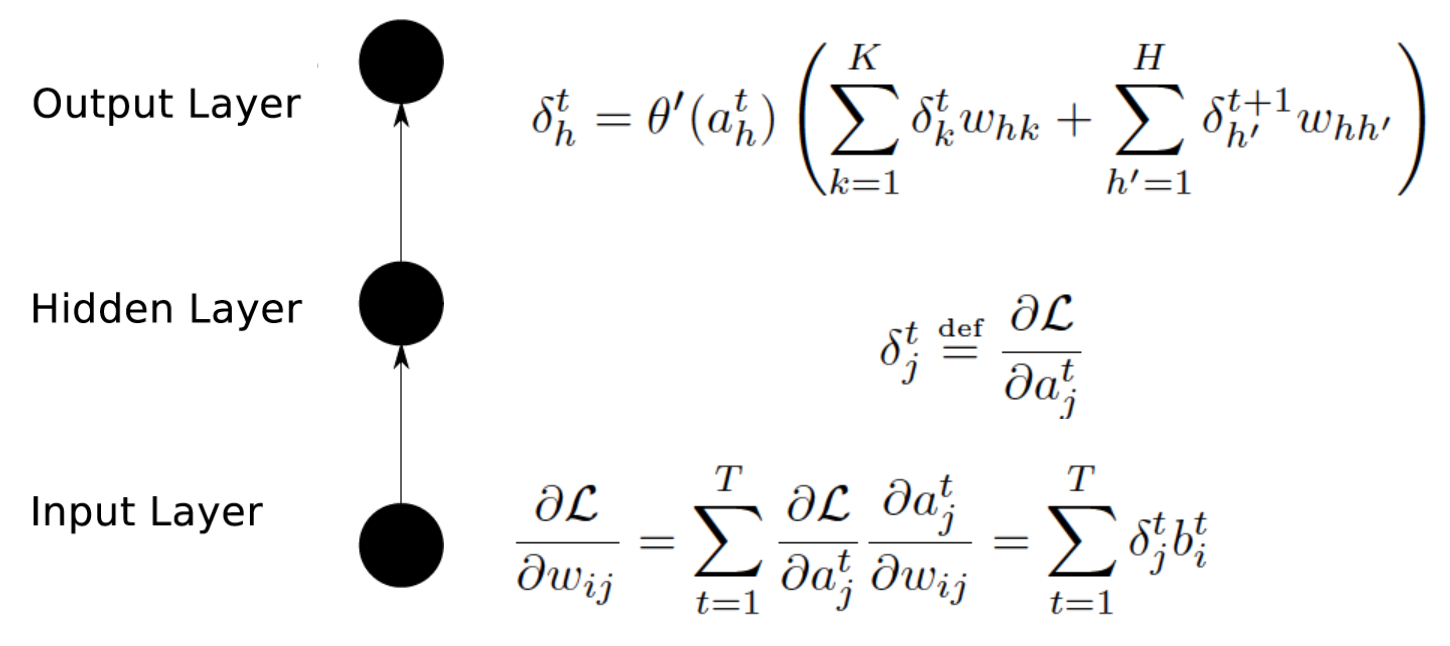
Forward Calculate

计算公式如下：

$\mathrm{s}_t=f(U\mathrm{x}_t+W\mathrm{s}_{t-1})$

$\mathrm{s}t$,$\mathrm{x}_t$,$\mathrm{s}{t-1}$都是向量
U、V是矩阵可用矩阵标示

$\begin{aligned} \begin{bmatrix} s_1^t\\ s_2^t\\ .\\.\\ s_n^t\\ \end{bmatrix}=f( \begin{bmatrix} u_{11} u_{12} ... u_{1m}\\ u_{21} u_{22} ... u_{2m}\\ .\\.\\ u_{n1} u_{n2} ... u_{nm}\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ .\\.\\ x_m\\ \end{bmatrix}+ \begin{bmatrix} w_{11} w_{12} ... w_{1n}\\ w_{21} w_{22} ... w_{2n}\\ .\\.\\ w_{n1} w_{n2} ... w_{nn}\\ \end{bmatrix} \begin{bmatrix} s_1^{t-1}\\ s_2^{t-1}\\ .\\.\\ s_n^{t-1}\\ \end{bmatrix}) \end{aligned}$

Calculate $\mathbf{ \Large { \frac{\partial{E}}{\partial{w_{ji}}}} }$

$\begin{aligned} \frac{\partial{E}}{\partial{w_{ji}}}=&\frac{\partial{E}}{\partial{net_j^t}}\frac{\partial{net_j^t}}{\partial{w_{ji}}}\\ =&\delta_j^ts_i^{t-1} \end{aligned}$

$\delta_j^t=\frac{\partial{E}}{\partial{net_j^t}}$ (refrence Calculate $\mathbf{ \delta_k^T }$)
$s_i^{t-1} =\frac{\partial{net_j^t}}{\partial{w_{ji}}}$
Calculate $\mathbf{ \Large { \delta_k^T} }$

$\begin{aligned} \delta_k^T =&\delta_t^T\prod_{i=k}^{t-1}Wdiag[f'(\mathrm{net}_{i})] [\mathbf{RP01}] \end{aligned}$

$net_t$表示神经元在t时刻的加权输入：

$\begin{aligned} \mathrm{net}_t&=U\mathrm{x}_t+W\mathrm{s}_{t-1}\\ \mathrm{s}_{t-1}&=f(\mathrm{net}_{t-1})\\ \end{aligned}$

Calcaulte $\mathbf{ { \nabla_WE}}$

$\nabla_WE= \sum_{i=1}^t\nabla_{W_i} [\mathbf{RP02}]$

Calcaulte $\mathbf{ { \nabla_UE}}$

$\nabla_UE=\sum_{i=1}^t\nabla_{U_i}E [\mathbf{RP03}]$

Grendient Dscent

single vaule calculate

$\begin{aligned} &Repeat\{ \\ &w_{ji}:= w_{ji}-\eta\frac{\Delta {E_d}}{\Delta {w_{ji}}} \\ &u_{ji}:= u_{ji}-\eta\frac{\Delta {E_d}}{\Delta {u_{ji}}} \\ &\} \end{aligned}$

matrix calculate

$\begin{aligned} &Repeat\{ \\ &W:=W-\eta\nabla_WE \\ &U:=U-\eta\nabla_UE \\ &\} \end{aligned}$

Reasoning Process

[01] Reasoning $\mathbf{\delta_k^T}$

$\begin{aligned} \delta_k^T=&\frac{\partial{E}}{\partial{\mathrm{net}_k}} \\ =&\frac{\partial{E}}{\partial{\mathrm{net}_t}}\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{net}_k}} \\ =&\frac{\partial{E}}{\partial{\mathrm{net}_t}}\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{net}_{t-1}}}\frac{\partial{\mathrm{net}_{t-1}}}{\partial{\mathrm{net}_{t-2}}}...\frac{\partial{\mathrm{net}_{k+1}}}{\partial{\mathrm{net}_{k}}} \\ =&Wdiag[f'(\mathrm{net}_{t-1})]Wdiag[f'(\mathrm{net}_{t-2})]...Wdiag[f'(\mathrm{net}_{k})]\delta_t^l \\ =&\delta_t^T\prod_{i=k}^{t-1}Wdiag[f'(\mathrm{net}_{i})] \end{aligned}$

计算误差项$\frac{\partial{\mathrm{net}t}}{\partial{\mathrm{net}{t-1}}}$

先计算第一项$\frac{\partial{\mathrm{net}t}}{\partial{\mathrm{s}{t-1}}}$

第一项是向量函数对向量求导，其结果为Jacobian矩阵：

$\begin{aligned} \frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{s}_{t-1}}}&=\begin{bmatrix}\frac{\partial{net_1^t}}{\partial{s_1^{t-1}}}& \frac{\partial{net_1^t}}{\partial{s_2^{t-1}}}& ...& \frac{\partial{net_1^t}}{\partial{s_n^{t-1}}}\\ \frac{\partial{net_2^t}}{\partial{s_1^{t-1}}}& \frac{\partial{net_2^t}}{\partial{s_2^{t-1}}}& ...& \frac{\partial{net_2^t}}{\partial{s_n^{t-1}}}\\ &.\\ &.\\ \frac{\partial{net_n^t}}{\partial{s_1^{t-1}}}& \frac{\partial{net_n^t}}{\partial{s_2^{t-1}}}& ...& \frac{\partial{net_n^t}}{\partial{s_n^{t-1}}}\\ \end{bmatrix}\\ &=\begin{bmatrix} w_{11} & w_{12} & ... & w_{1n}\\ w_{21} & w_{22} & ... & w_{2n}\\ &.\\ &.\\ w_{n1} & w_{n2} & ... & w_{nn}\\ \end{bmatrix}\\ &=W\end{aligned}$

再计算第二项$\frac{\partial{\mathrm{s}{t-1}}}{\partial{\mathrm{net}{t-1}}}$

第二项也是一个Jacobian矩阵：

$\begin{aligned} \frac{\partial{\mathrm{s}_{t-1}}}{\partial{\mathrm{net}_{t-1}}}&= \begin{bmatrix} \frac{\partial{s_1^{t-1}}}{\partial{net_1^{t-1}}}& \frac{\partial{s_1^{t-1}}}{\partial{net_2^{t-1}}}& ...& \frac{\partial{s_1^{t-1}}}{\partial{net_n^{t-1}}}\\ \frac{\partial{s_2^{t-1}}}{\partial{net_1^{t-1}}}& \frac{\partial{s_2^{t-1}}}{\partial{net_2^{t-1}}}& ...& \frac{\partial{s_2^{t-1}}}{\partial{net_n^{t-1}}}\\ &.\\&.\\ \frac{\partial{s_n^{t-1}}}{\partial{net_1^{t-1}}}& \frac{\partial{s_n^{t-1}}}{\partial{net_2^{t-1}}}& ...& \frac{\partial{s_n^{t-1}}}{\partial{net_n^{t-1}}}\\ \end{bmatrix}\\ &=\begin{bmatrix} f'(net_1^{t-1}) & 0 & ... & 0\\ 0 & f'(net_2^{t-1}) & ... & 0\\ &.\\&.\\ 0 & 0 & ... & f'(net_n^{t-1})\\ \end{bmatrix}\\ &=diag[f'(\mathrm{net}_{t-1})] \end{aligned}$

daig[a] 表示向量a创建一个对角矩阵

$diag(\mathrm{a})=\begin{bmatrix} a_1 & 0 & ... & 0\\ 0 & a_2 & ... & 0\\ &.\\&.\\ 0 & 0 & ... & a_n\\ \end{bmatrix}$

使用第一项&第二项计算误差项$\frac{\partial{\mathrm{net}t}}{\partial{\mathrm{net}{t-1}}}$

$\begin{aligned} \frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{net}_{t-1}}}&=\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{s}_{t-1}}}\frac{\partial{\mathrm{s}_{t-1}}}{\partial{\mathrm{net}_{t-1}}}\\ &=Wdiag[f'(\mathrm{net}_{t-1})]\\ &=\begin{bmatrix} w_{11}f'(net_1^{t-1}) & w_{12}f'(net_2^{t-1}) & ... & w_{1n}f(net_n^{t-1})\\ w_{21}f'(net_1^{t-1}) & w_{22} f'(net_2^{t-1}) & ... & w_{2n}f(net_n^{t-1})\\ &.\\&.\\ w_{n1}f'(net_1^{t-1}) & w_{n2} f'(net_2^{t-1}) & ... & w_{nn} f'(net_n^{t-1})\\ \end{bmatrix}\\ \end{aligned}$

02 Resoning $\mathbf{ { \nabla_WE}}$

$\begin{aligned} \nabla_WE=&\sum_{i=1}^t\nabla_{W_i} \\ =&\begin{bmatrix} \delta_1^ts_1^{t-1} & \delta_1^ts_2^{t-1} & ... & \delta_1^ts_n^{t-1}\\ \delta_2^ts_1^{t-1} & \delta_2^ts_2^{t-1} & ... & \delta_2^ts_n^{t-1}\\ .\\.\\ \delta_n^ts_1^{t-1} & \delta_n^ts_2^{t-1} & ... & \delta_n^ts_n^{t-1}\\ \end{bmatrix} +...+ \begin{bmatrix} \delta_1^1s_1^0 & \delta_1^1s_2^0 & ... & \delta_1^1s_n^0\\ \delta_2^1s_1^0 & \delta_2^1s_2^0 & ... & \delta_2^1s_n^0\\ .\\.\\ \delta_n^1s_1^0 & \delta_n^1s_2^0 & ... & \delta_n^1s_n^0\\ \end{bmatrix} \end{aligned}$

03 Resoning $\mathbf{ { \nabla_UE}}$

$\nabla_{U_t}E=\begin{bmatrix} \delta_1^tx_1^t & \delta_1^tx_2^t & ... & \delta_1^tx_m^t\\ \delta_2^tx_1^t & \delta_2^tx_2^t & ... & \delta_2^tx_m^t\\ .\\.\\ \delta_n^tx_1^t & \delta_n^tx_2^t & ... & \delta_n^tx_m^t\\ \end{bmatrix}$

基础神经网络&双向神经网络