Gradient Discent 梯度下降

梯度下降是降低损失的一个过程

• 步长（Learning rate）：步长决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度。用上面下山的例子，步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。
• 特征（feature）：指的是样本中输入部分，比如2个单特征的样本（x(0),y(0)）,（x(1),y(1)）,则第一个样本特征为x(0)，第一个样本输出为y(0)。
• 假设函数（hypothesis function）：在监督学习中，为了拟合输入样本，而使用的假设函数，记为hθ(x)。比如对于单个特征的m个样本（x(i),y(i)）(i=1,2,…m),可以采用拟合函数如下： hθ(x)=θ0+θ1x。
• 损失函数（loss function）：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平方。比如对于m个样本（xi,yi）(i=1,2,…m),采用线性回归，损失函数为:

$$J(\theta_0, \theta_1) = \sum\limits_{i=1}^{m}(h_\theta(x_i) - y_i)^2$$

　　　其中xi表示第i个样本特征，yi表示第i个样本对应的输出，hθ(xi)为假设函数

梯度下降的应用场景

如下以线性回归的梯度下降，作为说明

Line regression

• model

$$y=ax+b$$

• loss

$$loss=\frac{1}{2m}\sum_{i=1}^m(y_{p,i}-y_i)^2$$

Gradient Descent

• summary

$$\theta_{t+1}=\theta_{t}-\alpha\frac{df}{d\theta}$$

• process

$$\begin{aligned} &y_{p,i}=ax_i+b \\ &{loss=\frac{1}{2m}\sum_{i=1}^m(y_{p,i}-y_i)^2 } \\ &{loss=\frac{1}{m}\sum_{i=1}^m\frac12(ax_i+b-y_i)^2 } \\ \end{aligned}$$

• single process

$${loss_{i}=\frac{1}{2}(ax_i+b-y_i)^2 }$$

• partial diffrential

$$\begin{aligned} &\frac{\partial loss_{i}}{\partial a}=(ax_i+b-y_i)x_i \\ &\frac{\partial loss_{i}}{\partial b}=(ax_i+b-y_i) \\ \end{aligned}$$

• cumulation

$$\begin{aligned} &\frac{\partial loss}{\partial a}=\frac{1}{m}\sum_{i=1}^m\frac{\partial loss_{i}}{\partial a} \\ &\frac{\partial loss}{\partial b}=\frac{1}{m}\sum_{i=1}^m\frac{\partial loss_{i}}{\partial b} \\ \end{aligned}$$

• update param

$$\begin{aligned} &a_{new}=a-\alpha \nabla a \\ &b_{new}=b-\alpha \nabla b \\ \end{aligned}$$

梯度下降算法种类

BGD（Batch Gradient Descent） 批量梯度下降

每次使用全量的训练集样本来更新模型参数

$$\theta = \theta - \eta \cdot \nabla_{\theta}J(\theta)$$

算法特点

全量梯度下降每次学习都使用整个训练集，因此其优点在于每次更新都会朝着正确的方向进行，最后能够保证收敛于极值点(凸函数收敛于全局极值点，非凸函数可能会收敛于局部极值点)，但是其缺点在于每次学习时间过长，并且如果训练集很大以至于需要消耗大量的内存，并且全量梯度下降不能进行在线模型(模型数据一致在更新中）参数更新。

优点

• 全局最优解；易于并行实现

缺点

• 当样本数目很多时，训练过程会很慢

计算过程

• summary

$$\theta_{t+1}=\theta_{t}-\alpha\frac{df}{d\theta}$$

• process

$$\begin{aligned} &y_{p,i}=ax_i+b \\ &{loss=\frac{1}{2m}\sum_{i=1}^m(y_{p,i}-y_i)^2 } \\ &{loss=\frac{1}{m}\sum_{i=1}^m\frac12(ax_i+b-y_i)^2 } \\ \end{aligned}$$

• single process

$${loss_{i}=\frac{1}{2}(ax_i+b-y_i)^2 }$$

• partial diffrential

$$\begin{aligned} &\frac{\partial loss_{i}}{\partial a}=(ax_i+b-y_i)x_i \\ &\frac{\partial loss_{i}}{\partial b}=(ax_i+b-y_i) \\ \end{aligned}$$

• cumulation

$$\begin{aligned} &\frac{\partial loss}{\partial a}=\frac{1}{m}\sum_{i=1}^m\frac{\partial loss_{i}}{\partial a} \\ &\frac{\partial loss}{\partial b}=\frac{1}{m}\sum_{i=1}^m\frac{\partial loss_{i}}{\partial b} \\ \end{aligned}$$

• update param

$$\begin{aligned} &a_{new}=a-\alpha \nabla a \\ &b_{new}=b-\alpha \nabla b \\ \end{aligned}$$

SGD(Stochasitc Gradient Descent) 随机梯度下降

随机梯度下降算法每次从训练集中随机选择一个样本来进行学习

$$\theta = \theta - \eta \cdot \nabla_{\theta}J(\theta;x_i;y_i)$$

算法特点

优点

• 训练速度快

缺点

• 准确度下降，并不是全局最优；不易于并行实现

计算过程

• summary

$$\theta_{t+1}=\theta_{t}-\alpha\frac{df}{d\theta}$$

• process

$$\begin{aligned} &y_{p,i}=ax_i+b \\ &{loss=\frac{1}{2}(y_{p,i}-y_i)^2 } \\ \end{aligned}$$

• partial diffrential

$$\begin{aligned} & \frac{\partial loss}{\partial a}=(ax_i+b-y_i)x_i \\ & \frac{\partial loss}{\partial b}=(ax_i+b-y_i) \\ \end{aligned}$$

• update param

$$\begin{aligned} &a_{new}=a-\alpha \nabla a \\ &b_{new}=b-\alpha \nabla b \\ \end{aligned}$$

mini-batch SGD 小批量梯度下降

Mini-batch梯度下降综合了batch梯度下降与stochastic梯度下降，在每次更新速度与更新次数中间取得一个平衡，其每次更新从训练集中随机选择m,m<n个样本进行学习

$$\theta = \theta - \eta \cdot \nabla_{\theta}J(\theta;x_{i:i+m};y_{i:i+m})$$

计算过程

• summary

$$\theta_{t+1}=\theta_{t}-\alpha\frac{df}{d\theta}$$

• process

$$\begin{aligned} &y_{p,i}=ax_i+b \\ &{loss_{batch}=\frac{1}{2k}\sum_{i=1}^k(y_{p,i}-y_i)^2 } \\ \end{aligned}$$

k标示bach的总样本数

• partial diffrential

$$\begin{aligned} &\frac{\partial loss_{batch}}{\partial a}=\frac{1}{k}\sum_{i=1}^k(ax_i+b-y_i)x_i\\ &\frac{\partial loss_{batch}}{\partial b}=\frac{1}{k}\sum_{i=1}^k(ax_i+b-y_i) \\ \end{aligned}$$

• update param

$$\begin{aligned} &a_{new}=a-\alpha \nabla a \\ &b_{new}=b-\alpha \nabla b \\ \end{aligned}$$

Momentum 冲量梯度下降算法

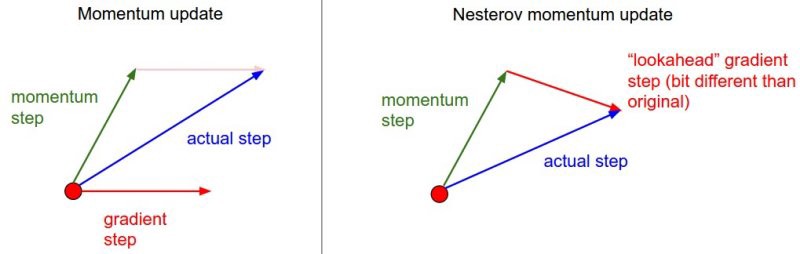
冲量梯度下降算法是BorisPolyak在1964年提出的，其基于这样一个物理事实：将一个小球从山顶滚下，其初始速率很慢，但在加速度作用下速率很快增加，并最终由于阻力的存在达到一个稳定速率。
momentum即动量，它模拟的是物体运动时的惯性，即更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向。这样一来，可以在一定程度上增加稳定性，从而学习地更快，并且还有一定摆脱局部最优的能力：

计算过程

• summary

$$\theta_{new} = \theta - \alpha\nabla a$$

• update param

$$\begin{aligned} &v_t = \gamma v_{t-1} + \alpha \nabla b \\ &\theta_{new} = \theta - v_t \\ \end{aligned}$$

γ , 0.9

NAG(Nesterov accelerated gradient)

NAG算法全称Nesterov Accelerated Gradient,是YuriiNesterov在1983年提出的对冲量梯度下降算法的改进版本，其速度更快。其变化之处在于计算“超前梯度”更新冲量项

计算过程

• summary

$$\begin{aligned} v0&=0 \\ v_1&=\eta \nabla_{\theta}J(\theta) \\ v_2&=\gamma v_1+\eta \nabla_{\theta}J(\theta-\gamma v_1) \\ &\downarrow \\ v_t&=\gamma v_{t-1}+\eta \nabla_{\theta}J(\theta-\gamma v_{t-1}) \\ \end{aligned}$$

• update param

$$\theta_{new} = \theta - v_t$$

Adagrad

AdaGrad是Duchi在2011年提出的一种学习速率自适应的梯度下降算法。在训练迭代过程，其学习速率是逐渐衰减的，经常更新的参数其学习速率衰减更快，这是一种自适应算法

算法特点

优点

• 前期gt较小的时候， regularizer较大，能够放大梯度
• 后期gt较大的时候，regularizer较小，能够约束梯度
• 适合处理稀疏梯度

缺点

• 仍依赖于人工设置一个全局学习率
• η设置过大的话，会使regularizer过于敏感，对梯度的调节太大
• 中后期，分母上梯度平方的累加将会越来越大，使gradient→0，使得训练提前结束

计算过程

• SGD的梯度下降

$$\Theta_{t+1,i} =\Theta_{t,i}-\alpha \cdot g_{t,i}$$

• update param
  每轮训练中对每个参数θi的学习率进行更新

$$\Theta_{t+1,i} =\Theta_{t,i}- \frac{\alpha}{\sqrt{G_{t,ii}+\epsilon }}\cdot g_{t,i}$$ $$G_{t,ii}=\sum_{r=1}^t(g_t)^2$$

RMSprop

RMSprop是Hinton在他的课程上讲到的，其算是对Adagrad算法的改进，主要是解决学习速率过快衰减的问题。其实思路很简单，类似Momentum思想，引入一个超参数，在积累梯度平方项进行衰减。

计算过程

• update param
  每轮训练中对每个参数θi的学习率进行更新，跟新方法不同

$$\begin{aligned} &E[g^2]_t=0.9E[g^2]_{t-1}+0.1g_t^2 \\ &\Theta_{t+1} =\Theta_{t}- \frac{\alpha}{\sqrt{E[g^2]_t+\epsilon }}\cdot g_{t} \\ \end{aligned}$$

Adam(Adaptive Moment Estimation)

Adam全称Adaptive moment estimation，是Kingma等在2015年提出的一种新的优化算法，其结合了Momentum和RMSprop算法的思想。相比Momentum算法，其学习速率是自适应的，而相比RMSprop，其增加了冲量项。所以，Adam是两者的结合体。

• 利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率

计算过程

$$\begin{aligned} m_t&=\beta_1m_{t-1}+(1-\beta_1)g_t \\ v_t&=\beta_1v_{t-1}+(1-\beta_1)g_t^2 \\ \hat{m}_t&=\frac{m_t}{1-\beta_1^t} \\ \hat{v}_t&=\frac{v_t}{1-\beta_2^t} \\ \Theta_{t+1}&=\Theta_{t}- \frac{\alpha}{\sqrt{\hat{v}_t }+\epsilon }\hat{m}_t \\ \end{aligned}$$

• 如tensolrflow的对应方法
  $python tf.train.AdamOptimizer(learning_rate=0.001,beta1=0.9, beta2=0.999, epsilon=1e-08)$

牛顿法（Newton method）

牛顿法的核心思想是”利用函数在当前点的一阶导数，以及二阶导数，寻找搜寻方向“（回想一下更简单的梯度下降法，她只用了当前点一阶导数信息决定搜索方向）。牛顿法的迭代公式是（稍微有修改，最原始的牛顿法γ=1：

$$ { {\bf{x}}_{n + 1}} = { {\bf{x}}_n} - \gamma {[Hf({ {\bf{x}}_n})]^{ - 1}}\nabla f({ {\bf{x}}_n})

$$ 其中，${[Hf({ {\bf{x}}_n})]^{ - 1}}\nabla f({ {\bf{x}}_n})$是线搜索方向。这个方向的含义是什么呢。有两种物理解释：

• 一阶导数∇f(x)当前搜寻点 与 ∇f(x)=0连线的方向。
• 当前点泰勒展开（舍弃二阶以上项）函数中 当前搜寻点 与 泰勒展开函数极小值连线方向。

  拟牛顿法（Quasi-Newton method）

  上述的牛顿法需要计算Hessian矩阵的逆矩阵，运算复杂度太高。在动辄百亿、千亿量级特征的大数据时代，模型训练耗时太久。因此，很多牛顿算法的变形出现了，这类变形统称拟牛顿算法。拟牛顿算法的核心思想用一个近似矩阵B替代逆Hessian矩阵$H^{-1} $的矩阵B的计算有差异，但大多算法都是采用迭代更新的思想在tranning的没一轮更新矩阵B。

DFP,BFGS,L-BFGS

BFGS

BFGS(Broyden–Fletcher–Goldfarb–Shanno)的算法流程如下：

1. 初始化：初始点x0以及近似逆Hessian矩阵$B_0^{ - 1}$。通常，${B_0} = I$,既为单位矩阵。
2. 计算线搜索方向：${ {\bf{p}}_k} = - B_k^{ - 1}\nabla f({ {\bf{x}}_k})$
3. 用”Backtracking line search“算法沿搜索方向找到下一个迭代点：${ {\bf{x}}_{k + 1}} = { {\bf{x}}_k} + {\alpha _k}{ {\bf{p}}_k}$
4. 根据Armijo–Goldstein 准则，判断是否停止。
5. 计算${ {\bf{x}}{k + 1}} = { {\bf{x}}_k} + {\alpha _k}{ {\bf{p}}_k}$ 以及 ${ {\bf{y}}_k} = \nabla f({ {\bf{x}}{k + 1}}) - \nabla f({ {\bf{x}}_k})$
6. 迭代近似逆Hessian矩阵：

$$B_{k + 1}^{ - 1} = \left( {I - \frac{ { {s_k}y_k^T}}{ {y_k^T{s_k}}}} \right)B_k^{ - 1}\left( {I - \frac{ { {y_k}s_k^T}}{ {y_k^T{s_k}}}} \right) + \frac{ { {s_k}s_k^T}}{ {y_k^T{\mkern 1mu} {s_k}}}$$

L-BFGS

BFGS算法需要存储近似逆Hessian矩阵$B_0^{-1}$。对于很多应用来说（比如百度的CTR预估），千亿量级的feature数需要$10^{16}$p存储。显然，目前的计算机技术还很难满足这样的空间需求。因此，内存受限的BFGS算法(Limited-memory BFGS)就诞生了。

OWL-QN

OWL-QN算法的全称是Orthant-Wise Limited-memory Quasi-Newton。从全称可以看出，该算法是单象限的L-BFGS算法，也就是说，OWL-QN算法每次迭代都不会超出当前象限。

共轭梯度法(Conjugate Gradient)

---

• Previous
  逻辑回归
• Next
  激活函数