词向量

Word Embdding & Gram 词向量&Gram模型

Word Eembdding 词向量

NPLM（Neural Probablistic Language Model）神经概率语言模型

语言模型 词串是${w_t}_{t=1}^T=w_1^T=w_1,w_2,…,w_T$自然语言的概率$P(w_1^T)$

$w_t$下标 t 表示其是词串中的第 t 个词

• 根据乘法规律计算整个词串概率：

$$P(w_1,w_2,...,w_T)=P(w_1)P(w_2|w_1)P(w_3|w_1,w_2)...P(w_T|w_1,w_2,...,w_{T-1})$$

• 先计算单个词的概率$P(w_t

  w_1,w_2,…,w_{t-1}),t\in {1,2,…,T}$：

$$P(w_t|w_1,w_2,...,w_{t-1})=\frac{\text{count}(w_1,w_2,...,w_{t-1},w_t)}{\text{count}(w_1,w_2,...,w_{t-1})}$$

count()是指词串在语料中出现的次数

$$\begin{aligned}P(w_t|w_1,w_2,...,w_{t-1})&\approx P(w_t|w_{t-(n-1)},w_{t-(n-2)},...,w_{t-1})\\&=\frac{\text{count}(w_{t-(n-1)},w_{t-(n-2)},...,w_{t-1},w_t)}{\text{count}(w_{t-(n-1)},w_{t-(n-2)},...,w_{t-1})}\end{aligned}$$

目标词 $w_t$ 的条件概率只与其之前的 n−1 个词有关

训练语言模型 $w$
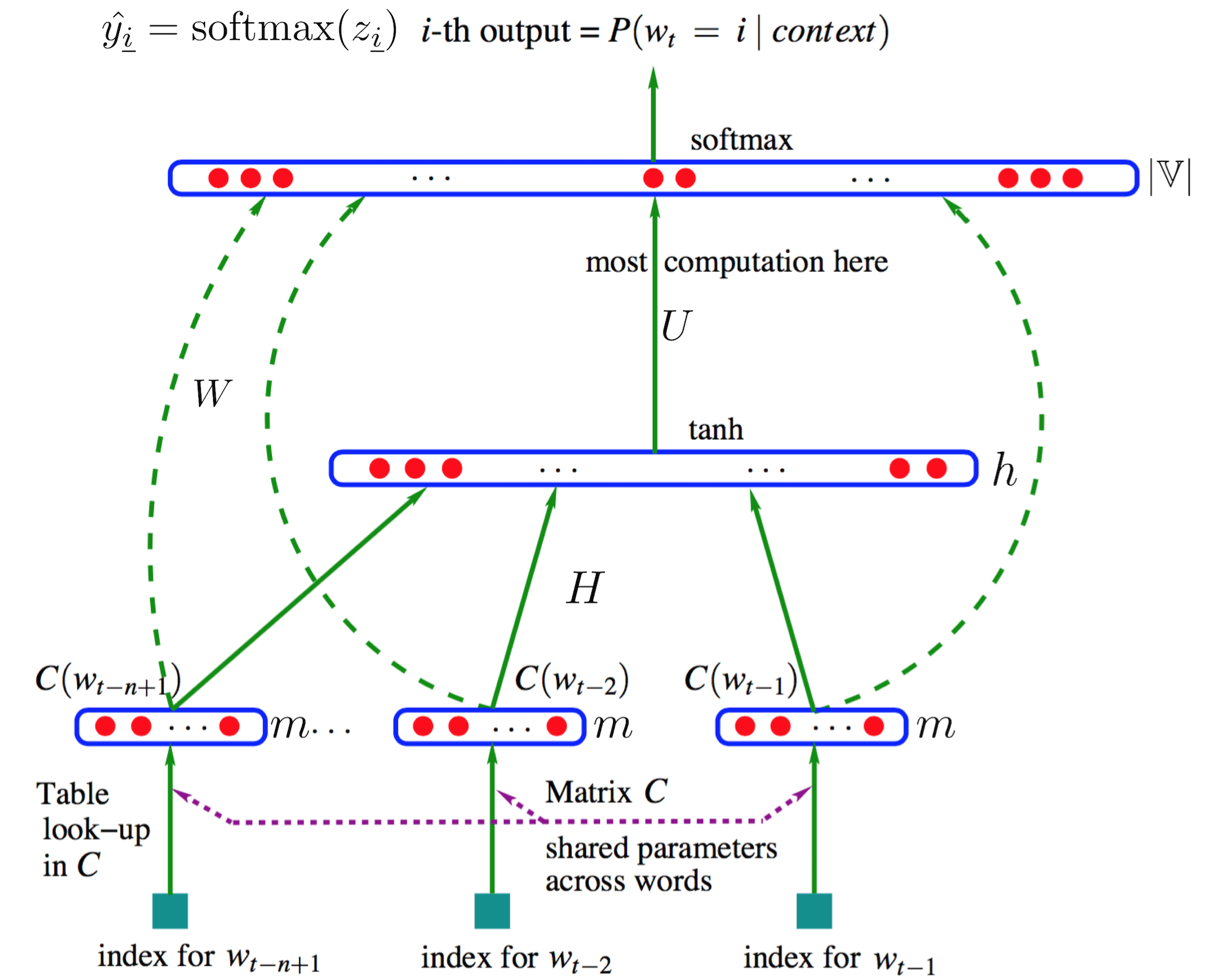
1，将语料中的一个词串 $w_{t-(n-1)}^t$ 的目标词 $w_t$之前的 n−1 个词的词向量（即word embedding，设维度为 m ）按顺序首尾拼接得到一个“长”的列向量 x ，作为输入层（也就是说共 (n−1)m 个神经元）
2，然后经过权重矩阵$H_{h\times (n-1)m}$来到隐层（神经元数为 h ），并用tanh函数激活
3，再经过权重矩阵 $U_{|\mathbb V|\times h}$ 来到输出层（神经元数当然为 |V| ），并使用softmax()将其归一化为概率
4，另外存在一个从输入层直连输出层的权重矩阵$W_{|\mathbb V|\times (n-1)m}$

$$z=U\tanh (Hx+d)+b+Wx$$ $$\hat y_{\underline i}=P(w_{\underline i}|w_{t-(n-1)},w_{t-(n-2)},...,w_{t-1})=\text{softmax}(z_{\underline i})=\frac{\exp z_{\underline i}}{\sum\limits_{k=1}^{|\mathbb V|}\exp z_{\underline k}},\quad w_{\underline i}\in \mathbb V$$

$\hat y_{\underline i}$ 表示目标词是词表中第 i 个词$w_i$的概率
$\exp z_{\underline i}$ 表示前 n−1 个词对词表中第 i 个词$w_i$的能量聚集

训练参数
需要参数有$C,U,H,W,b,d$

• 叉熵损失函数,模型对于目标词wt的损失为

$$\mathcal L =-\log \hat y_t=-\log P(w_t|w_{t-(n-1)},w_{t-(n-2)},...,w_{t-1})=-\log \text{softmax}(z_t)$$

• 整个模型的损失为

$$\begin{aligned} \mathcal L&=-\sum_{w_{t-(n-1)}^t\in \mathbb D}\log \hat y_t\\&=-\sum_{w_{t-(n-1)}^t\in \mathbb D}\log P(w_t|w_{t-(n-1)},w_{t-(n-2)},...,w_{t-1})\\&=-\sum_{w_{t-(n-1)}^t\in \mathbb D}\log \text{softmax}(z_t) \end{aligned}$$

N-Gram N元祖模型

给定的一段文本(Item可以是音节、字母、单词)来评估此句子，N=1时称为unigram，N=2称为bigram，N=3称为trigram，以此类推. 人们基于一定的语料库，可以利用N-Gram来预计或者评估一个句子是否合理。另外一方面，N-Gram的另外一个作用是用来评估两个字符串之间的差异程度。这是模糊匹配中常用的一种手段

假设由m个单子的句子，我们来评估此句子的概率：

$$P(w_1, w_2, \cdots, w_m)=P(w_1)P(w_2|w_1)P(w_3|w_1,w_2)\cdots P(w_m|w_1,\cdots ,w_{m-1})$$

这个概率的计算量太大，可以使用马尔科夫链的假设，即当前这个词仅仅跟前面N个有限的词相关，因此也就不必关心到最开始的那个词，可以减少大量的计算量

$$P(w_i| w_1, \cdots, w_{i-1})=P(w_i|w_{i-n+1},\cdots ,w_{i-1})$$

• 当N=1时，unigram

$$P(w_1, w_2, \cdots, w_m)=\prod_{i=1}^mP(w_i)$$

• 当N=2时，biggram

$$P(w_1, w_2, \cdots, w_m)=\prod_{i=1}^mP(w_i|w_{i-1})$$

• 当N=3时，trigram

$$P(w_1, w_2, \cdots, w_m)=\prod_{i=1}^mP(w_i|w_{i-2}w_{i-1})$$

后续的做法，可以利用最大似然法来求出一组参数，使得训练样本的概率取得最大值.

• 对于unigram model而言，其中c(w1,..,wn) 表示 n-gram w1,..,wn 在训练语料中出现的次数，M 是语料库中的总字数（例如对于 yes no no no yes 而言，M=5）

$$P(w_i)=\frac{C(w_i)}{M}$$

• 对于 biggram

$$P(w_i|w_{i-1})=\frac{C(w_{i-1}w_i)}{C(w_{i-1})}$$

• 对于 n gram

$$P(w_i|w_{i-n-1},\cdots, w_{i-1})=\frac{C(w_{i-n-1},\cdots, w_{i})}{C(w_{i-n-1},\cdots, w_{i-1})}$$

CBOW Continuous Bag of Words

从上下文来预测一个文字

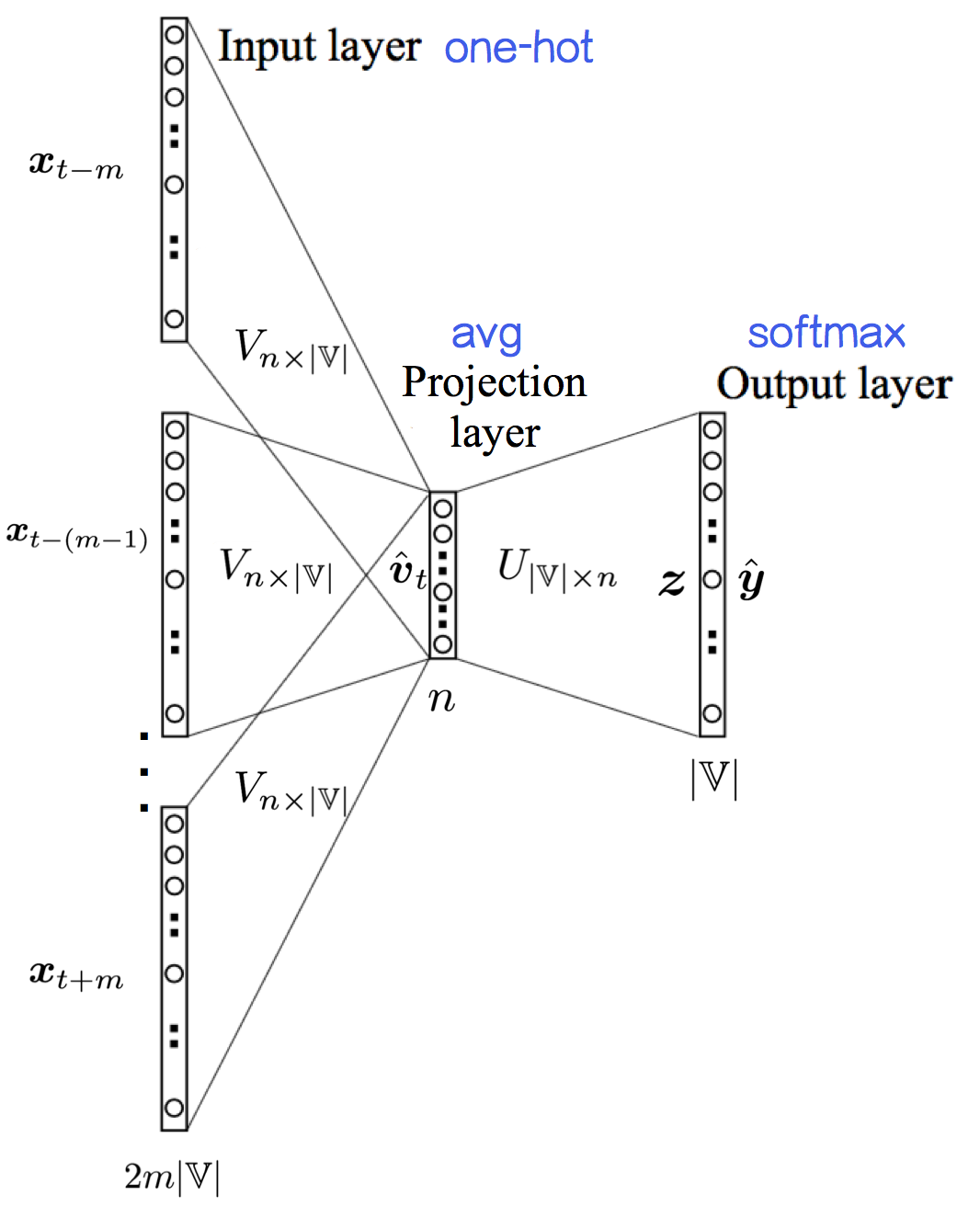
• 输入层：2m×|V|个节点，上下文共 2m个词的one-hot representation
• 输入层到投影层到连接边：输入词矩阵$V_{n\times \mathbb V }$
• 投影层：：n个节点，上下文共 2m个词的词向量的平均值；
• 投影层到输出层的连接边：输出词矩阵$U_{\mathbb V\times n}$
• 输出层：|V|个节点

训练步骤

• 将中心词 wt 的上下文 $w_{t-m},…,w_{t-1},w_{t+1},…,w_{t+m}$由one-hot representation($x_{t+j}$)转为输入词向量($v_{t+j}$)

$$v_{t+j}=V x_{t+j},\quad j\in \{-m,...,m\}\setminus \{0\}$$

• 上下文的输入词向量$ v_{t-m},…,v_{t-1}, v_{t+1},…,v_{t+m}$求平均值，作为模型输入

$$\hat{ v}_t=\frac{1}{2m}\sum_j v_{t+j},\quad j\in \{-m,...,m\}\setminus \{0\}$$

这一步叫投影（projection）。可以看出，CBOW像词袋模型(BoW)一样抛弃了词序信息，然后窗口在语料上滑动，就成了连续词袋= =。丢掉词序看起来不太好，不过开个玩笑的话：“研表究明，汉字的序顺并不定一能影阅响读，事证实明了当你看这完句话之后才发字现都乱是的”

• softmax()输出目标词是某个词的概率

$$z=U\hat{ v}_t$$ $$\hat y_{\underline i}=P(w_{\underline i}|w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m})=\text{softmax}(z_{\underline i})=\text{softmax}( u_{\underline i}^\top \hat{ v}_t),\quad w_{\underline i}\in \mathbb V$$

• 中心词 $w_t$ ，模型对它的损失

$$\begin{aligned}\mathcal L&=-\log \hat y_t\\&=-\log P(w_t|w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m})\\&=-\log \text{softmax}(z_t)\\&=-\log \frac{\exp (u_t^\top \hat{ v}_t)}{\sum_{k=1}^{|\mathbb V|}\exp ( u_{\underline k}^\top \hat{ v}_t)}\\&=- u_t^\top \hat{v}_t+\log \sum_{k=1}^{|\mathbb V|}\exp ( u_{\underline k}^\top \hat{ v}_t)\\&=-z_t+\log \sum_{k=1}^{|\mathbb V|}\exp z_{\underline k} \end{aligned}$$

• 计算对于整个模型的损失

$$\begin{aligned} \mathcal L&=-\sum_{w_{t-m}^{t+m}\in \mathbb D}\log \hat{y_t}\\&=-\sum_{w_{t-m}^{t+m}\in \mathbb D}\log P(w_t|w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m})\\&=-\sum_{w_{t-m}^{t+m}\in \mathbb D}\log \text{softmax}(z_t) \end{aligned}$$

Skip-Gram

从一个文字来预测上下文 image

CBOW模型把上下文的 2m 个词向量求平均值“揉”成了一个向量 $\hat{ v}t$ 然后作为输入，进而预测中心词；而Skip-gram模型则是把上下文的 2m 个词向量$ v{t+j}$ 依次作为输入，然后预测中心词

少了一个计算平均值的过程，多了计算的次数

训练步骤

• 中心词 $w_t$ ，模型对它的损失

$$\begin{aligned}\mathcal L&=-\log P(w_t|w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m})\\&=-\log \prod_jP(w_t|w_{t+j})\\&=-\log \prod_j\hat y_t^{(j)}\\&=-\log \prod_j\text{softmax}(\hat z_t^{(j)})\\&=-\sum_j\log \frac{\exp ( u_t^\top v_{t+j})}{\sum\limits_{k=1}^{|\mathbb V|}\exp ( u_{\underline k}^\top v_{t+j})}\end{aligned}$$

Refrence

https://www.cnblogs.com/Determined22/p/5804455.html

---

• Previous
  距离计算
• Next
  主题生成模型